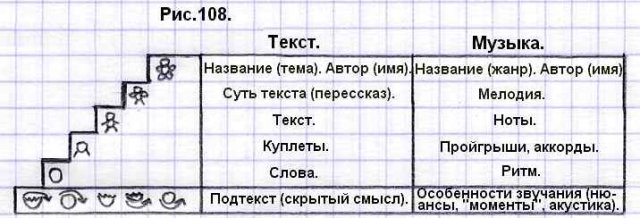
. В прошлом топике мы разделили информацию на дискретные порции: Л, 1/2Л+1/2А, А, Л*А, Л*А+Л*А, указав, что люди различаются по способности воспринимать тот или иной объём информации, обучаться и думать соответствующими категориями. Все исследования проводились популяризировано, позволяя на словах разобраться в разнице мышления исполнителей, заведующих производств, директората и учёных с гениями. В данном же топике мы перейдём к математическим моделям, докажем дискретность типа мышления, разберём понятие "чернорабочий" с наличием половинчатой логикой или же анализа.
. Прежде чем переходить к скучной для женщин абстрактной математике и намного более интересному табличному описанию типов мышления людей вернёмся несколько назад, акцентируя внимания на отличии между исполнителями и директоратом. Ведь разница мышления требующего намёка двоечника и мыслящего формулами учёного очевидна для всех, не требует особых доказательств.
. Где же та грань, когда накопив большее число вариантов решения одной и той же задачи человек превращается сначала в заведующего, а потом и в делового человека? Ведь и достаточно опытный исполнитель может выполнить поручаемое ему задание разными способами, что делает его мышление как бы похожим на директора.
. Сам по себе перебор механических вариантов решения задачи не является аналитическим складом ума. Даже зная сотню способов исполнитель ни когда не станет деловым. Более того, уже в 5-7 лет разница между способами мышления очевидна, сохраняется всю жизнь с небольшими изменениями. Просмотр мультфильмов или же чтение книг с фантастическим сюжетом приводит делового в восторг, т.к. такие варианты ему ни когда не приходили в голову. Тогда как исполнителю больше нравятся погони и драки, как и он в принципе мог бы поступить. Проявляя интерес к решению задачи при помощи физической силы и всевозможных вариаций её воплощения или же к гипотетическим возможностям науки и техники навсегда разделяет ценности и стремления повзрослевших людей.
. Например, какой-то из детей целый день способен играть с маленьким игрушечным автомобилем. Благодаря богатой фантазии, которая позволяет всё нас окружающее использовать в разных сферах деятельности, ему не скучно: одалживал друзьям на выходные, продавал, покупал, угонял, совершал грабежи, воевал, ремонтировал, ездил за границу, даже летал в космос подобии Гарри Поттера. Автомобиль использовался не только как транспортное средство, но и как повод для участия в социальной жизни общества под разными личинами, включая и «научную сферу» из учёных и естествоиспытателей. Другой же ребёнок, покидав многие надоевшие игрушки, устремляется бегать и прыгать с машинкой в руках, т.к. мысленно использовал все возможности езды, включая даже и ДТП с каскадёрством.
. Данный топик начался с перечисления дискретных способов мышления, были даже всевозможные математические вариации описания: Л, 1/2Л+1/2А, А, Л*А, Л*А+Л*А. Соответствует ли это реалиям, либо ещё один «учёный от психологии» приводит какие-то ни кому не понятные, выдуманные абстрактные величины? Статья о термине «логика» из Википедии. Одна из главных задач логики — определить, как прийти к выводу из предпосылок, неполных данных и получить истинное знание о предмете размышления. В любой науке логика служит одним из основных инструментов.
Таким образом логика представляет из себя всего лишь узнавание. Правда это касается не только вещей и людей, с чем легко справляется даже и ребёнок, но и происходящих процессов. Изобразим всё графически в виде точек, которые будут символизировать перечень каких-то характеристик единого предмета - вершины.
.
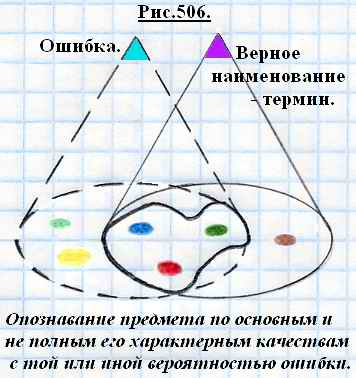
. Например, с точки зрения логики детская загадка о двух концах и двух кольцах с находящимся посередине гвоздиком является крайне сложной задачей для узнавания предмета - ножниц, т.к. кольца носят на руках в виде украшения, а гвоздик относится к строительству. Одновременно перепутать с чем-то нет возможности даже и взрослому, т.к. к верному ответу более ни чего не подходит.
. Благодаря формулировке понятия двухмерности мышления мы знаем, что люди неспособны мысленно объединять многие различные описательные характеристики какого-то предмета, а только парами. Кроме того выяснили, что существуют базовые «кирпичики» из секса, еды и убежища, которые объединяясь между собой дают более сложные понятия всего и вся нас окружающего. Таким образом получаем, что каждой верхней точке нашего будущего математического графика изображения способа мышления человека будут соответствовать минимум две точки нижних уровней. Увеличиваясь в объёме информация будет располагаться всё время всё выше и выше, пока не достигнет какого-то предела (рис.505в).
.

В продолжении топика строго научно изучим уровни графика, что из себя представляет самая верхняя точка. Понимая о необходимости времени на размышление выясним, что же будет ординатой, какова её размерность. Пока же для интереса представим анализ в виде формулы, сознавая, что на графике всё выглядеть будет компактнее и информативнее: Л+Л+Л+…+Л = А
.





 Войти
Войти Регистрация
Регистрация














 Наверх
Наверх